UPDATES: May 2017
Roadside Swale Infiltration Performance Calculator
May 2017 (volume 12 - issue 1)
Contributed by Maria del Carmen Garcia de la Serrana Lozano, Ph.D.; John S. Gulliver, Professor, St. Anthony Falls Laboratory and the Department of Civil, Environmental, and Geo-Engineering, University of Minnesota, and John L. Nieber, Professor, Department of Bioproducts and Biosystems Engineering, University of Minnesota.
Funded by the Minnesota Department of Transportation (MnDOT), Minnesota Local Road Research Board (LRRB).
Introduction
The rising levels of urbanization are associated with hydrological impacts and stress on urban drainage systems (Booth and Jackson, 1997; Fletcher et al., 2012). There is a trend in stormwater management towards practices that try to restore the site’s predevelopment hydrology. Such practices are called Low Impact Development (LID) or Green Infrastructure (GI) and are typically designed to reduce runoff volumes and improve runoff water quality.
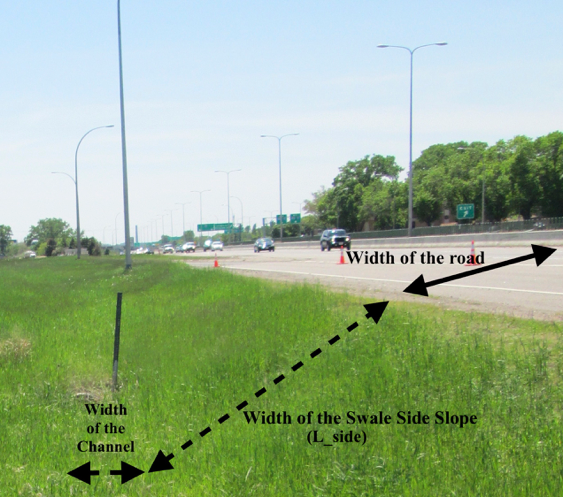
There are approximately 2.2 million acres of grassland in the Right-of-way of the National Highway System in the United States (USDOT-FHWA, 2010). Grassed roadside drainage ditches or swales (Figure 1) convey and treat water by sedimentation and filtration of solid particles (sediment-bound nutrients), and infiltration of stormwater and dissolved pollutants in the runoff water (Abida and Sabourin, 2006). Therefore, grassed roadside swales are stormwater management practices and can be considered LID or GI. Volume reduction of roadway runoff occurs primarily through infiltration into the soil, either as the water flows over the side slope (which acts as a filter strip) or down the length of the swale channel parallel to the roadway. There is a growing interest in stormwater calculators that quantify reductions in runoff for roadside swales. Our goal was to develop a calculator that allows the user to estimate the total percentage of annual volume infiltrated or the percentage of events captured by a roadside swale based on a few essential input parameters: lengths of the road and the swale, saturated hydraulic conductivity of the soil, and the location’s percentile rainfall volume or frequency.
Figure 1: Roadside Swale on Hwy 77 in Richfield, MN USA.
Methods
A numerical model developed by Garcia-Serrana et al. (2017b) simulates overland flow and infiltration over roadside swales. The model is based on the Green-Ampt-Mein-Larson assumptions to calculate infiltration along with a kinematic wave model for overland flow that accounts for concentrated flow (flow in “fingers”). The roadside swale model was validated using the data collected in twelve simulated runoff tests for three different highways (Hwy 13, 51, and 77) located in the Minneapolis-St. Paul metropolitan area, MN USA (Garcia-Serrana et al., 2017a).
However, the main disadvantage of the Garcia-Serrana et al. model is the number of input parameters required. A simplified model has been developed to obtain easy and fast approximations of the performance of these runoff management practices, identifying the most important parameters. In order to find these parameters, two global sensitivity analyses (Morris, 1991; Pianosi and Wagener, 2015) were performed. Based on the results of the sensitivity analyses, the volume infiltrated by a roadside swale is most sensitive to the saturated hydraulic conductivity (Ksat); which is in agreement with previous studies on filter strip models. The model outputs are also somewhat sensitive to soil wetting front suction pressure (Ψ) and soil moisture deficit (Δθ). However, effective wetting front suction changes with soil moisture content and the soil moisture content fluctuates throughout a season, while computations of percent infiltrated will be based upon the hydrology of many seasons. For this reason, the two parameters (Ψ, Δθ) have been fixed to a representative value observed in the field (Garcia-Serrana et al., 2017a). The rest of the parameters: Manning’s n, channel width, slope, fraction wetted, and depression storage, are not as critical for calculating infiltration performance of roadside swales, therefore average values have been assigned for the simplified calculations.
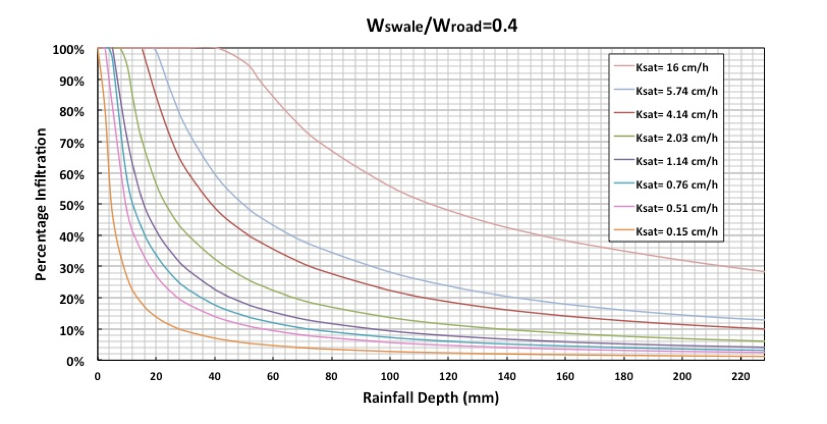
Simulations of the model were repeated with different values of Ksat and ratios of width of the roadside filter strip over width of the road (Wswale/Wroad). The outputs were used to quantify the relationship between rainfall depth of one storm and percentage infiltration for a wide range of input values. An example of these relationships is shown in Figure 2 for a Wswale/Wroad = 0.4 and Ksat ranging from 0.15 to 16cm/h.
Figure 2: Rainfall depths versus percentage infiltration for a ratio of width of the swale side (Wswale) over width of the road (Wroad) of 0.4. The eight curves represent different saturated hydraulic conductivities.
The second piece of information needed to determine annual infiltration performance of roadside swales is the distribution of the annual rainfall of the specific site. Therefore, additional inputs of the model are either the percentile rainfall volume and/or frequency curves; these represent the percentage exceedance in terms of annual volume or total number of rainfall events. The percentage of total annual precipitation that will be infiltrated in a particular roadside swale can then be calculated by multiplying each of the probabilities of a certain rainfall event to happen (based on total depth) times the percentage infiltration for the specific rainfall depth and design characteristics (Ksat and Wswale/Wroad).
Results
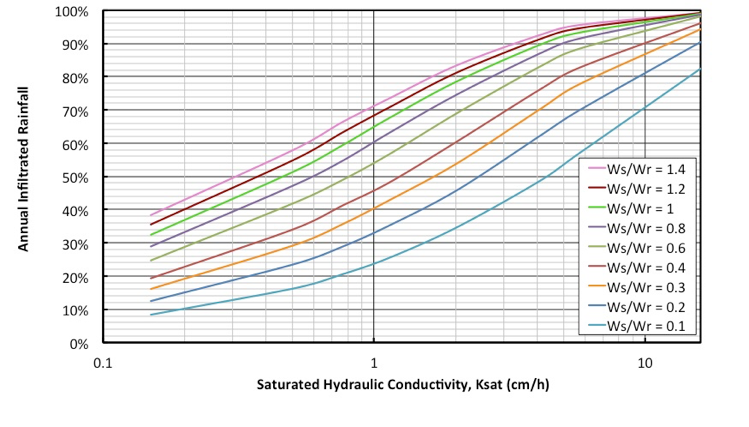
The simplified model, or roadside swale infiltration performance calculator, is in an Excel spreadsheet. The inputs needed are: 1) location’s percentile rainfall volume or frequency, 2) width of the swale side slope, 3) width of the road, and 4) Ksat of the roadside swale’s soil. The results consist of a numerical quantification of the annual infiltration performance of roadside swales and a graphical illustration of the results for different scenarios of design characteristics (Wswale/Wroad) or soil properties (Ksat) (Figure 3).
Figure 3: Annual infiltration performances versus saturated hydraulic conductivity (Ksat) based on the Minneapolis - St. Paul, MN International airport rainfall station Minneapolis - St. Paul, MN International airport rainfall station.
Conclusions
A roadside swale calculator has been generated based on the results obtained with an extended model that simulates the overland flow and infiltration processes on swales. The input parameters have been proven to be essential to obtain accurate results based on the results of two global sensitivity analyses. The swale and soil characteristics needed to run the calculator are Wswale/Wroad ratio and Ksat value. This practical calculator is suitable for design and planning purposes, answering three main questions:
- What total percentage of annual volume is infiltrated by roadside swales?
- What percentage of annual rainfall events is captured by this stormwater management practice?
- What infiltration percentage in a single event is achieved by a roadside swale for a given rainfall depth?
For answering the first two questions, the Excel calculator needs input of the percentile of rainfall volume or frequency of a specific site, respectively. The third question can be answered based on the curves (e.g., Figure 2) that relate percentage infiltration of a rainfall event of a given depth to Ksat, for a specific Wswale/Wroad ratio. This calculator enables designers and planners to directly determine a Wswale/ Wroad ratio that will achieve a desired level of infiltration efficiency for a design storm.
Download the Calculator:
http://stormwater.safl.umn.edu/resources/roadside-swale-calculator.
Watch the Seminar:
https://umn.webex.com/umn/ldr.php?RCID=a0ea17201dfa7048081bfc17af36bd76.
References
- Abida H. and Sabourin, J. F. (2006). Grass swale-perforated pipe systems for stormwater management. Journal of Irrigation and Drainage Engineering, 132(1), 55-63.
- Booth, D. B. and Jackson, C. R. (1997). Urbanization of Aquatic Systems: Degradation Thresholds, Storm Water Detection, and the Limits of Mitigation. Journal of the American Water Resources Association, 33(5): 1077–1090.
- Fletcher, T. D., Andrieu, H., and Hamel, P. (2013). Understanding, management and modelling of urban hydrology and its consequences for receiving waters; a state of the art. Advances in Water Resources, 51, 261–279.
- Garcia-Serrana, M., Gulliver, J. S., Nieber, J. L. 2017a Infiltration Capacity of Roadside Filter Strips with Non-Uniform Overland Flow. Journal of Hydrology, 545(2): 451–462.
- Garcia-Serrana, M., Gulliver, J. S., Nieber, J. L. 2017b Non-Uniform Overland Flow-Infiltration Model for Roadside Swales. (under revision).
- Morris, M. D. (1991) Factorial sampling plans for preliminary computational experiments. Technometrics, 33(2): 161–174.
- Pianosi, F. and Wagener, T. (2015). A simple and efficient method for global sensitivity analysis based on cumulative distribution functions. Environmental Modelling & Software, 67: 1–11.
- U.S. Department of Transportation - Federal Highway Administration (2010). Carbon Sequestration Pilot Program. Estimated Land Available for Carbon Sequestration in the National Highway System. Federal Highway Administration Office of Planning, Environment and Realty, Washington, DC, USA.